搜索
1.定义
搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况,从而求出问题的解的一种方法。现阶段一般有枚举算法、深度优先搜索、广度优先搜索、A* 算法、回溯算法、蒙特卡洛树搜索、散列函数等算法。在大规模实验环境中,通常通过在搜索前,根据条件降低搜索规模;根据问题的约束条件进行剪枝;利用搜索过程中的中间解,避免重复计算这几种方法进行优化。(来自百度百科)
2.运行原理
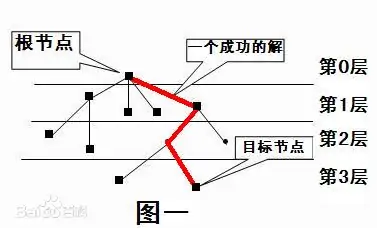
搜索算法实际上是根据初始条件和扩展规则构造一棵“解答树”并寻找符合目标状态的节点的过程。不同的搜索算法不同的只是拓展节点的方式和拓展的节点,而所有的算法优化和改进主要都是通过修改其控制结构来完成的。其实,在这样的思考过程中,我们已经不知不觉地将一个具体的问题抽象成了一个图论的模型——树,即搜索算法的使用第一步在于搜索树的建立
由图可以知道,这样形成的一棵树叫搜索树。初始状态对应着根节点,目标状态对应着目标结点。排在前的结点叫父结点,其后的结点叫子结点,同一层中的结点是兄弟结点,由父结点产生子结点叫扩展。完成搜索的过程就是找到一条从根结点到目标结点的路径,找出一个最优的解。这种搜索算法的实现类似于图或树的遍历,通常可以有两种不同的实现方法,即深度优先搜索(DFS——Depth First search)和广度优先搜索(BFS——Breadth First Search)。
3.主要类别
深度优先搜索(dfs)
深度优先搜索,顾名思义,即尽可能向深处进行搜索,即选定一条确定的路径,不断地向子节点进行搜索,直到到达末节点或者到达答案,并且在探索过程中,一旦发现原来的选择不符合要求,就回溯至父亲结点重新选择另一结点,继续向前探索,如此反复进行,直至求得最优解。深度优先搜索的实现方式可以采用递归或者栈来实现。
相关剪枝思想
为了缩短搜索时间我们可以想到一些方法去减搜索的纸条,从而减少节点的搜索,主要可以从以下几点出发
(1)减少节点数,思想:尽可能减少生成的节点数
(2)定制回溯边界,思想:定制回溯边界条件,剪掉不可能得到最优解的子树
在我们平时看来显而易见不可能出现最优解的情况对于计算机而言,仍然会去搜索,判断,因此我们需要合理使用剪枝条,排除掉一些不可能出现最优解的情况,这也同样是后期学习搜索需要考虑的方法
广度优先搜索(bfs)
广度优先搜索,主要的点在于广字上,它与深度优先搜索的不同在于,深度优先搜索是一搜到底的搜索,而广度优先搜索在于广泛,其过程为:首先访问初始点Vi,并将其标记为已访问过,接着访问Vi的所有未被访问过可到达的邻接点Vi1、Vi2……Vit,并均标记为已访问过,然后再按照Vi1、Vi2……Vit的次序,访问每一个顶点的所有未被访问过的邻接点,并均标记为已访问过,依此类推,直到图中所有和初始点Vi有路径相通的顶点都被访问过为止。
换而言之,广度优先搜索是一层一层的搜索,而深度优先搜索是一条线直接到底,相比而言,在部分情况下广度优先搜索有着更好的性能,部分情况下则是深度优先搜索,下面我们将讲解何时应该使用广度优先搜索,而何时应该使用深度优先搜索。
下面则是一些优化(在本文中不具体讲述各种搜索优化,只作为入门引入)

3.例题
P1149 [NOIP2008 提高组] 火柴棒等式

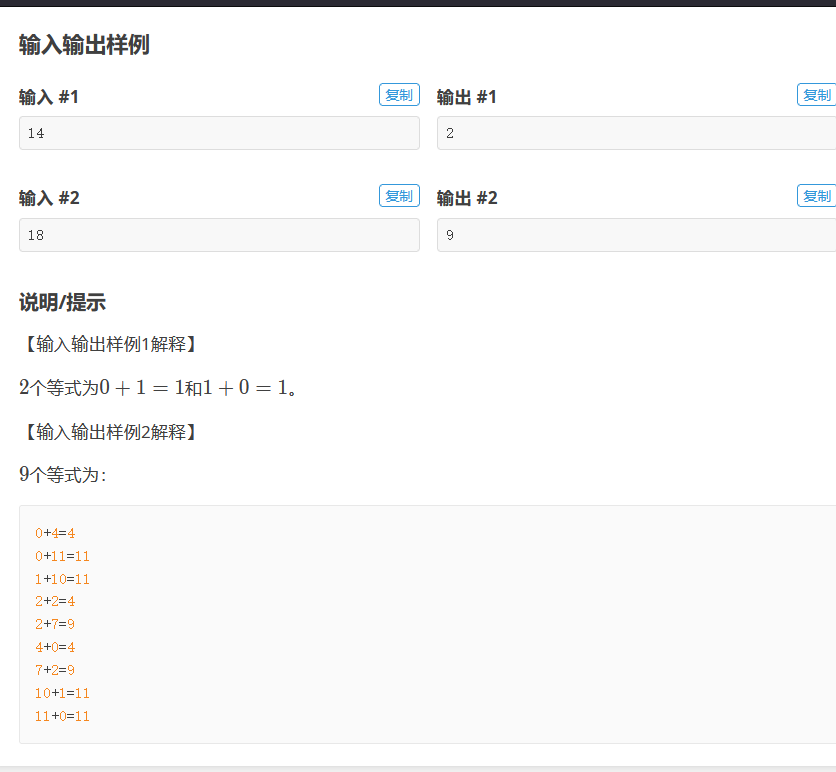
对于这道题目,我们可以发现,它给出所拥有的火柴棒个数,要求得出可能方案,也就是说无论使用广搜还是深搜都是需要搜遍整棵搜索树的,然而如果使用bfs,我们不方便判断每一层划分的参数,同样我们不能立即减去不可能出现的情况,因此我们这题使用的是深搜。
#include<bits/stdc++.h>
using namespace std;
int n,ans,a[15000]={6,2,5,5,4,5,6,3,7,6,8},book[10];
void dfs(int num,int data){
if(num>3){
if(book[1]+book[2]==book[3]&&!data){
ans++;
//printf("%d+%d=%d\n",book[1],book[2],book[3]);
}
return;
}
for(int i=0;i<=1111;++i){
if(a[i]<=data){
book[num]=i;
dfs(num+1,data-a[i]);
book[num]=-1;
}
}
}
int main(){
scanf("%d",&n);
if(n<=10) printf("0");
else{
//memset(book,-1,sizeof(book));
for(int i=11;i<=1111;++i){
a[i]=a[i/10]+a[i%10];
}
dfs(1,n-4);
printf("%d",ans);
}
return 0;
}解决搜索题目大致思路
1.确定使用哪种搜索方法
2.确定函数所带变量
3.确认临界条件
4.下一步搜索与回溯
在搜索前,我们需要做一系列的预处理,即得出每一个数字所出现所需要的火柴数,我们又知道只要我们知道了前10个数字,那么我们变掌握的所有的数字所需要的火柴棒。
并且我们可以先思考到一个数最大可以有多大,首先减去符号位 4 便是 20 其次,一个数需要进行加法,而最少的火柴棒便是1 即 1111+1111=2222
其次我们开始设定搜索所需要的参数,第一个是目前在寻找第几个数,而第二个意味着还有多少根火柴棒。接着,我们需要确定临界条件,对于 num 如果我们当前寻找的数大于3,那么说明我们已经寻找完毕,同时我们需要判断此时剩下的火柴棒是否为0即可。紧接着我们进行下一步搜索与回溯,即如何找到下一个数字,我们可以进行一次遍历,将所有符合当前火柴棒的数字全部都进行一次搜索即可。同时进行记录与回溯。
P1219 [USACO1.5]八皇后 Checker Challenge

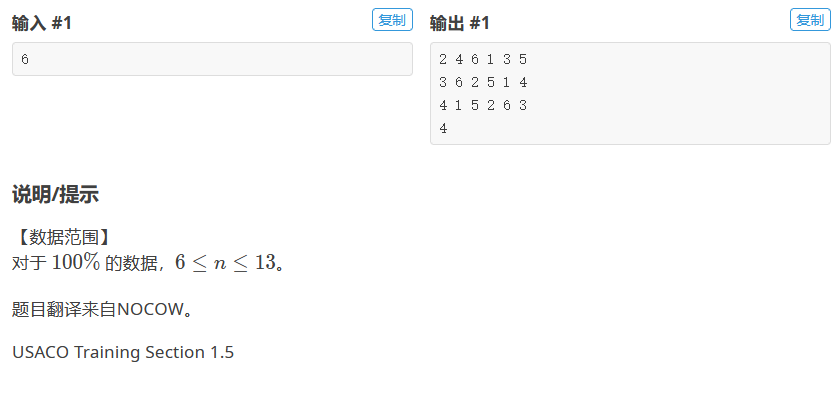
对于这道题目,我们同样使用的是深搜,即不断尝试每一个棋子的位置,并对其进行回溯。
#include<bits/stdc++.h>
using namespace std;
int n,ans,a[100],b[100],c[100],d[100];
void out(){
if(ans<=2){
for(int i=1;i<=n;++i){
printf("%d ",a[i]);
}
printf("\n");
}
ans++;
}
void dfs(int x){
if(x>n){
out();
return;
}
for(int j=1;j<=n;++j){
if((!b[j])&&(!c[x+j])&&(!d[x-j+n])){
a[x]=j;
b[j]=1;
c[x+j]=1;
d[x-j+n]=1;
dfs(x+1);
a[x]=0;
b[j]=0;
c[x+j]=0;
d[x-j+n]=0;
}
}
}
int main(){
scanf("%d",&n);
dfs(1);
printf("%d",ans);
return 0;
} 我们先确定变量,对于每一行我们都只能放一个棋子,那么我们可以将行数作为变量,而当行数大于当前所给出的n,那么说明已经搜索完毕,对于此题,在行数确定的情况下,我们只需要不断尝试每一列可以放在哪里即可,此时需要进行一次判断,判断这一列以及其所在对角线是否可行,我们通过观察可以发现 左对角线的编号可以写作(x+j),而右对角线可以写作 (x-j+n),则我们找到一个合理存在的点,并对其进行放置,并且标记它所在的列,对角线后进行下一次搜索以及回溯。
同样对于这题,我们可以用二进制数来表示状态,而不是用数组,原理是二进制数本身可以看作一个bool 类型的数组,有0/1 两种形式,可以用来表示状态。
#include<bits/stdc++.h>
using namespace std;
int n,add,book,line,data,ans[10];
bool getbit(int x,int i){
return !((x>>i)&1);
}
void dfs(int m){
if(m==n+1){
add++;
if(add<=3){
for(int i=1;i<=n;i++){
printf("%d",ans[i]);
if(i<n) printf(" ");
}printf("\n");
}
}
else{
for(int i=1;i<=n;i++){
if(getbit(line,i)&&getbit(data,i-m+n)&&getbit(book,i+m-1)){
line|=(1<<i);
book|=(1<<(i+m-1));
data|=(1<<(i-m+n));
ans[m]=i;
dfs(m+1);
line&=~(1<<i);
book&=~(1<<(i+m-1));
data&=~(1<<(i-m+n));
}
}
}
return;
}
int main(){
scanf("%d",&n);
dfs(1);printf("%d",add);
return 0;
} 此处涉及部分二进制运算,可以百度查看 二进制
P1451 求细胞数量
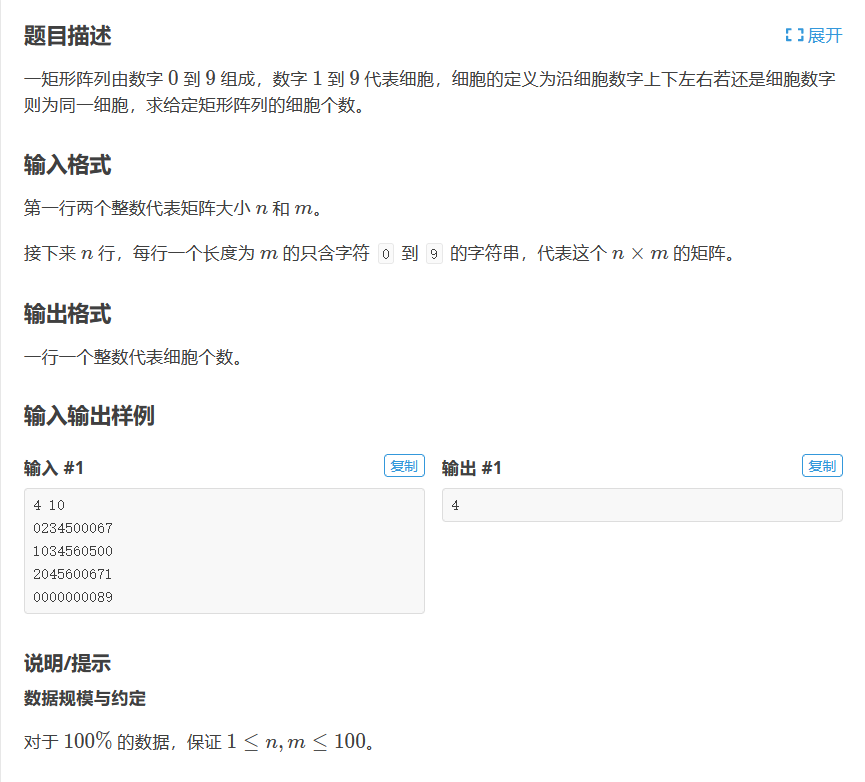
对于这题,我们需要从一个点向其它点进行扩散,判断是否为一个细胞,而深搜只能一搜到底。
#include<bits/stdc++.h>
using namespace std;
const int dx[4]={0,1,0,-1};
const int dy[4]={1,0,-1,0};
int m,n,ans;
int mp[101][101];
int vis[101][101];
struct node
{
int x,y;
};
queue <node> q;
void bfs(int x,int y)
{
node sta;
sta.x=x;
sta.y=y;
q.push(sta);
vis[x][y]=1;
while(!q.empty())
{
node fr=q.front();
vis[fr.x][fr.y]=1;
q.pop();
for(int i=0;i<4;i++)
{
node son;
son.x=fr.x+dx[i];
son.y=fr.y+dy[i];
if(mp[son.x][son.y]==0||vis[son.x][son.y])
continue;
else if(mp[son.x][son.y]&&(!vis[son.x][son.y]))
{
q.push(son);
}
}
}
return;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<m;j++)
{
scanf("%1d",&mp[i][j]);
if(mp[i][j]>0)
mp[i][j]=1;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(mp[i][j]&&(!vis[i][j])){
bfs(i,j);
ans++;
}
}
}
cout<<ans+1;
return 0;
}对于广搜,我们需要使用一个队列,来进行储存进行搜索的顺序,即当一个点搜索完毕的时候,将与它相邻的其它点加入队列进行下一次搜索并且重复上述过程。
首先是预处理,将细胞数字全部标记为 1,紧接着对于每一个为1的点进行搜索,判断周围的点是否为1,并且加入队列,不断进行扩散。参数为点的横纵坐标即可。此处注意广搜并不需要回溯这步操作,而只需要将点加入队列即可。
P1256 显示图像

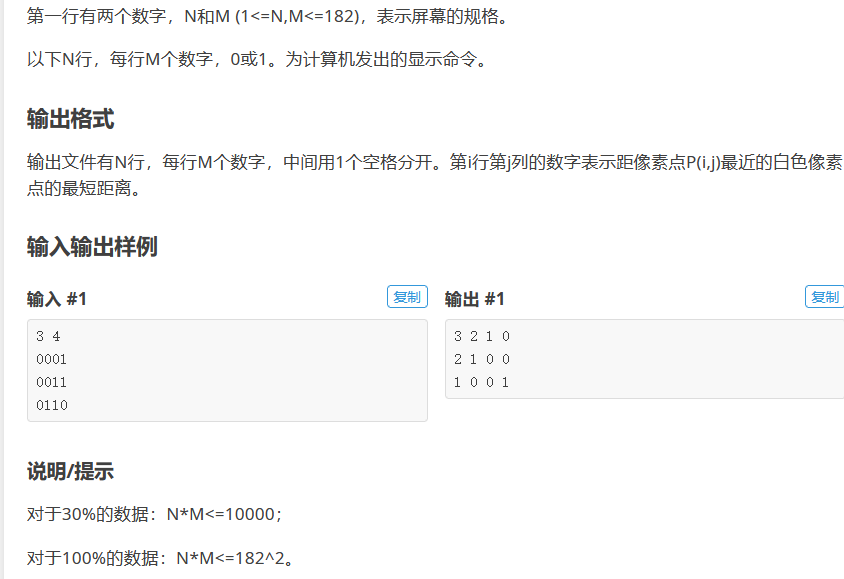
此处的思路与上述思路相近,不做过多阐述,直接放代码
#include<bits/stdc++.h>
using namespace std;
struct node{
int x;
int y;
};
node queu[40000];
const int dx[4]={-1,0,1,0};
const int dy[4]={0,1,0,-1};
int a[200][200],n,m,ans[200][200],l=1,r=1;
void bfs(){
if(l>r) return;
int nowx=queu[l].x;
int nowy=queu[l].y;
a[nowx][nowy]=1;
for(int i=0;i<4;++i){
int wx=nowx+dx[i];
int wy=nowy+dy[i];
if(!a[wx][wy]&&wx>=1&&wy>=1&&wx<=n&&wy<=m){
r++;
queu[r].x=wx;
queu[r].y=wy;
ans[wx][wy]=ans[nowx][nowy]+1;
a[wx][wy]=1;
}
}
l++;
bfs();
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%1d",&a[i][j]);
if(a[i][j]){
queu[r].x=i;
queu[r].y=j;
ans[i][j]=0;
r++;
}
}
}
bfs();
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
printf("%d ",ans[i][j]);
}
printf("\n");
}
return 0;
} 总结一下,对于搜索题目大致分为下面四步
1.确定使用哪种搜索方法
2.确定函数所带变量
3.确认临界条件
4.下一步搜索与回溯(对于广搜则为加入队列)