矩阵快速幂计算斐波那契数列

通过矩阵快速幂将100w位的斐波那契数列计算时间降低到4ms，时间复杂度 O(logN)

斐波那契数列递推公式（这里取从第二项开始）：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)

用矩阵表示：

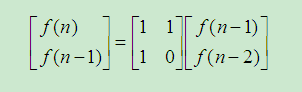
可以写出递归表达：

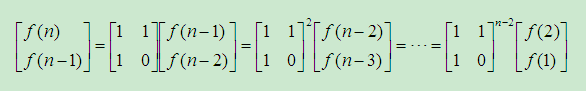
由计算到第n项为：

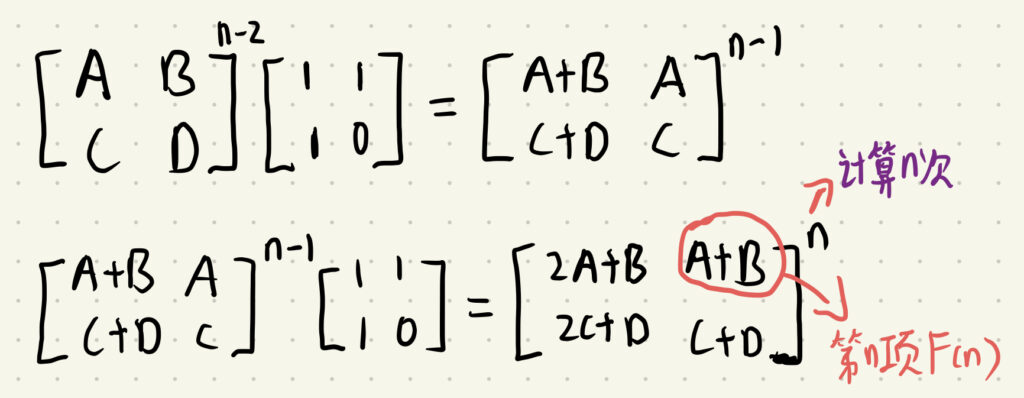
还要介绍按位与运算：&

a&1可以用来检测是否为奇数，当为奇数时结果为1，偶数为0。按位与是将两个数按位比较，同1则1。

下面看代码

#include <iostream>
#include <cstring>
using namespace std;

const int maxn = 2; //阶数
const int mod = 998244353;

//矩阵结构体
struct ma //matrix矩阵
{
    long long int a[maxn][maxn];
    void init()
    { //初始化为单位矩阵
        memset(a, 0, sizeof(a));
        for (int i = 0; i < maxn; ++i)
            a[i][i] = 1;
    }
};

//矩阵乘法
ma mul(ma a, ma b)
{
    ma ans;
    for (int i = 0; i < maxn; ++i)
    {
        for (int j = 0; j < maxn; ++j)
        {
            ans.a[i][j] = 0;
            for (int k = 0; k < maxn; ++k)
            {
                ans.a[i][j] += a.a[i][k] * b.a[k][j];
                ans.a[i][j] %= mod;      //这里mod了一个数，因为结果要mod998244353（题目要求）
            }
        }
    }
    return ans;
}

//矩阵快速幂
ma qpow(ma a, long long int n)
{
    ma ans;
    ans.init();
    while (n)
    {
        if (n & 1)          //后文会解释
            ans = mul(ans, a);
        a = mul(a, a);
        n /= 2;
    }
    return ans;
}

int main()
{       
    long long int n;
    ma a;
    a.a[0][0] = 1;
    a.a[0][1] = 1;
    a.a[1][0] = 1;
    a.a[1][1] = 0;
    cin >> n;
    ma ans = qpow(a, n);
    cout << ans.a[0][1]; //第n个斐波那契数
    return 0;
}

对求矩阵快速幂的原理解释，

假设求解10的75次方：

现在就是要求对二阶矩阵的n次方

ma qpow(ma a, long long int n)
{
    ma ans;
    ans.init();
    while (n)
    {
        if (n & 1)          
            ans = mul(ans, a);    //第一次使用单位矩阵相乘，结果不变
        a = mul(a, a);   //计算偶数次方，将时间复杂度将为lg（n）
        n /= 2;    //除到最后一定为奇数
    }
    return ans;
}

n为奇数时，ans = mul(ans, a) 会将n拆解成n/2+1和n/2，其中n/2是2的指数次，例如2的2次，2的4次，2的8次。比如，计算第15位的F时，最后的结果相当于将二阶矩阵的15次方拆解成7次和8次，便于计算。

如果看不太懂可以自己调试一下，很容易就理解了。

---