LITTLE SHOP OF FLOWERS
Description
You want to arrange the window of your flower shop in a most pleasant way. You have F bunches of flowers, each being of a different kind, and at least as many vases ordered in a row. The vases are glued onto the shelf and are numbered consecutively 1 through V, where V is the number of vases, from left to right so that the vase 1 is the leftmost, and the vase V is the rightmost vase. The bunches are moveable and are uniquely identified by integers between 1 and F. These id-numbers have a significance: They determine the required order of appearance of the flower bunches in the row of vases so that the bunch i must be in a vase to the left of the vase containing bunch j whenever i < j. Suppose, for example, you have bunch of azaleas (id-number=1), a bunch of begonias (id-number=2) and a bunch of carnations (id-number=3). Now, all the bunches must be put into the vases keeping their id-numbers in order. The bunch of azaleas must be in a vase to the left of begonias, and the bunch of begonias must be in a vase to the left of carnations. If there are more vases than bunches of flowers then the excess will be left empty. A vase can hold only one bunch of flowers.
Each vase has a distinct characteristic (just like flowers do). Hence, putting a bunch of flowers in a vase results in a certain aesthetic value, expressed by an integer. The aesthetic values are presented in a table as shown below. Leaving a vase empty has an aesthetic value of 0.
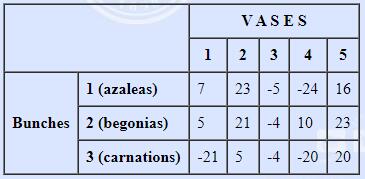
According to the table, azaleas, for example, would look great in vase 2, but they would look awful in vase 4.
To achieve the most pleasant effect you have to maximize the sum of aesthetic values for the arrangement while keeping the required ordering of the flowers. If more than one arrangement has the maximal sum value, any one of them will be acceptable. You have to produce exactly one arrangement.
Input
- The first line contains two numbers: F, V.
- The following F lines: Each of these lines contains V integers, so that Aij is given as the jth number on the (i+1)st line of the input file.
- 1 <= F <= 100 where F is the number of the bunches of flowers. The bunches are numbered 1 through F.
- F <= V <= 100 where V is the number of vases.
- -50 <= Aij <= 50 where Aij is the aesthetic value obtained by putting the flower bunch i into the vase j.
Output
The first line will contain the sum of aesthetic values for your arrangement.
Sample Input
3 5 7 23 -5 -24 16 5 21 -4 10 23 -21 5 -4 -20 20
Sample Output
53
我的代码
第i号花只能放在第i号到第v-f+i号花瓶内,那么给出dp[i][j]表示第i号花放在第j号花盆内所能产生的最大价值,其中j=i&&j<=v-f+i。dp[i][j]=value[i][j]+max(dp[i-1][k]),即指第i号花放在第j号花盆的最大价值对于其自身价值+第i-1号花盆所能产生的最大价值。
#include<stdio.h>
int info[101][101];
int dp[101][101];
int max(int x,int y)
{
return x>y?x:y;
}
int main()
{
int f,v;
scanf("%d%d",&f,&v);
for (int i=1;i<=f;i++)
{
for (int j=1;j<=v;j++)
{
scanf("%d",&info[i][j]);
}
}
for (int i=1;i<=v-1;i++)
{
dp[1][i]=info[1][i];
}
for (int i=2;i<=f;i++)
{
for (int j=i;j<=v-f+i;j++)
{
int temp=-1000000;
for (int k=i-1;k<j;k++)
{
temp=max(temp,dp[i-1][k]);
}
dp[i][j]=temp+info[i][j];
}
}
int ans=-1000000;
for (int i=f;i<=v;i++)
{
ans=max(ans,dp[f][i]);
}
printf("%d",ans);
return 0;
}正常思路
dp[i][j]记录前i朵花放在前j个花瓶中产生的最大价值。那么dp[i][j] = max(dp[i-1][j-1]+value[i][j],dp[i][j-1]),当i==j时 dp[i][j] = dp[i-1][j-1]+w[i][j]。
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;
const int maxn =100+10;
int flo_vas[maxn][maxn];
int dp[maxn][maxn];
int f,v;
int main()
{
scanf("%d%d",&f,&v);
memset(flo_vas,0,sizeof(flo_vas));
memset(dp,0,sizeof(dp));
for(int i=1;i<=f;++i)
for(int j=1;j<=v;++j)
scanf("%d",&flo_vas[i][j]);
for(int i=1;i<=f;++i)
for(int j=i;j<=v;++j)
{
if(i==j) dp[i][j]=dp[i-1][j-1]+flo_vas[i][j];
else dp[i][j]=max(dp[i-1][j-1]+flo_vas[i][j],dp[i][j-1]);
}
printf("%d\n",dp[f][v]);
return 0;
}反思
很明显我的算法多了一个循环,并且这一题也是很常规的一道题目,我却没有想到最常规的解法。我发现我用动规的思路往往和一般情况不同,我对于状态的转换过程还是考虑的太狭隘了,没有能够从全局进行考虑:比如这一题,并不需要考究一朵花具体要放在哪个花瓶里面,只需要考虑这些花整体的情况。