注:本篇内容转自程序设计基础的PPT,部分添加注释便于理解。
问题描述:
给定 n 个作业的集合 j = {j1, j2, …, jn}。每一个作业 j[i] 都必须先由机器1处理,然后由机器2处理。作业 j[i] 需要机器 j 的处理时间为 t[j][i] ,其中i = 1, 2, …, n, j = 1, 2。对于一个确定的作业调度,设F[j][i]是作业 i 在机器 j 上的完成处理的时间。所有作业在机器2上完成处理的时间之和 称为该作业调度的完成时间之和。
问题分析:
批处理作业调度是要从 n 个作业的所有排列中找出有最小完成时间和的作业调度,所以批处理调度问题的解空间是一棵排列树。按照回溯法搜索排列树的算法框架,设开始时x = [1, .., n]是所给的 n 个作业,则相应的排列树由所有排列构成。
批处理作业调度问题要求对于给定的 n 个作业,制定最佳作业调度方案,使其完成时间和达到最小。
| tji | 机器1 | 机器2 |
| 作业1 | 2 | 1 |
| 作业2 | 3 | 1 |
| 作业3 | 2 | 3 |
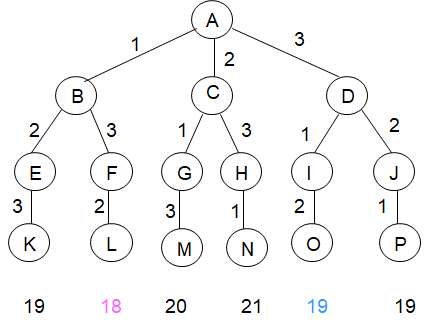
6种可能的调度方案是1,2,3;1,3,2;2,1,3;2,3,1;3,1,2;3,2,1;
相应的完成时间和分别是19,18,20,21,19,19。
易见,最佳调度方案是1,3,2,其完成时间和为18。
以1,2,3为例:
注意这里变成了Fji ,表示完成时间。
| Fji | 机器1 | 机器2 |
| 作业1 | 2 | 3 |
| 作业2 | 5 | 6 |
| 作业3 | 7 | 10 |
作业1在机器1上完成的时间为2,在机器2上完成的时间为3
作业2在机器1上完成的时间为5,在机器2上完成的时间为6
作业3在机器1上完成的时间为7,在机器2上完成的时间为10
3+6+10=19,所以是19。
以2,3,1为例:
| Fji | 机器1 | 机器2 |
| 作业2 | 3 | 4 |
| 作业3 | 5 | 8 |
| 作业1 | 7 | 9 |
作业2在机器1上完成的时间为3, 在机器2上完成的时间为4
作业3在机器1上完成的时间为5,在机器2上完成的时间为8
作业1在机器1上完成的时间为7,在机器2上完成的时间为9
4+8+9=21,所以时间和为21。
我的理解
由123和231这两个例子可以看出,当前作业2的完成时间F[j][2]为
F[j][2]=max(F[j][1],F[j-1][2])+t[j][2]
也就是当前作业的机器1完成时间和上一个作业机器2的完成时间中的最大值+当前作业机器2所需的时间。
核心代码:
void Flowshop::Backtrack(int i)
// x当前作业调度,bestx当前最优作业调度;
f完成时间和,bestf当前最优值。 {
if (i > n) { //达到出口条件,将结果保存输出
for (int j = 1; j <= n; j++) bestx[j] = x[j];
bestf = f;
} else
for (int j = i; j <= n; j++) {
f1 += M[x[j]][1]; // M[][]作业处理时间 f1表示机器1的完成时间和
f2[i] = ((f2[i - 1] > f1) ? f2[i - 1] : f1) + M[x[j]][2]; //F[j][2]计算 //f2[i]为机器2 第i个作业完成的时间
f += f2[i]; //f表示完成的总时间和
if (f < bestf) { //总时间比当前最短时间还小,剪枝
Swap(x[i], x[j]); //交换第j个作业和第i个作业
Backtrack(i + 1); //进入下层
Swap(x[i], x[j]); //还原
}
f1 - = M[x[j]][1]; //回退上一个节点
f - = f2[i];
}
}