会场安排问题

贪心算法有一道很经典的例题：会场安排问题。

该问题有两种变形：

第一种

只有一个会场，需要尽可能的安排更多场次的活动。题目具体描下

第二种

给出若干个活动，要求使用最少的会场数目。题目描述如下

假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。设计一个有效的 贪心算法进行安排。（这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个 顶点，不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数，相应于要找的最小 会场数。）

思路说明

第一种

该问题是很基础的贪心算法。主要思路是，按照结束时间最早的活动优先安排；意义是使剩余的可安排时间段极大化，以便安排尽可能多的相容活动。

代码如下：

template<class Type>
void GreedySelector(int n, Type s[], Type f[], bool A[])
{//s数组存储活动起始时间，数组存储活动结束时间，且各活动按结束时间E按非减序排列; A数组存储被选中的活动。
 A[1]=true; // 选择活动1 (结束最早的活动)
 int j=1; // j记录最近一次被选中的活动
 for (int i=2;i<=n;i++) 
 {
  if (s[i]>=f[j]) { A[i]=true; j=i; }
  else A[i]=false;
 } // 每次总是选择具有最早完成时间的相容活动加入集合A中
}

第二种

该问题看上去是可以看作多次调用第一种的方法来解决，即每一次会场都尽可能安排最多的会议数量，那么最终所要求的会场数一定是最少的。

这种贪心看似可行，实则不对。因为按照最早结束时间来安排一个会场，可能会产生两个活动之间间隔过长的情况。这样反而会使得所需要发会场数量增加。

这道题只要求总共所需的会场数最少，并不关注单个会场究竟最多可以安排几个活动。那么我们可以认为，一个会场如果它这个活动安排得十分紧凑，也就是上一个活动的结束时间与下一个活动开始时间相隔最短，这个会场的安排是更合理的。而按照之前的算法可能不能保证每一个会场都很紧凑。

下图就列举了一个例子（这个例子我修改了第三次才总算举对了）来证明第一种算法在第二题中是不可行的。

按照第一种算法的思路，以结束时间顺序来安排活动。那么一共需要三个会场，且会场1的选择是活动S1、S3。很显然的S1与S3之间的间隔太大，很明显是不紧凑的安排方法。这一种不紧凑的安排方式也使得最终所需要的会场数不是最少。就按照图上的例子而言，其实只要两个会场就够了：会场1安排活动S1、S4，会场2安排活动S2、S3。

因此此题不可套用第一题解法，而应该考虑去构造使得每一个会场都能最为紧凑的算法。

具体算法

我搜集了两种算法，现依次进行说明。

第一种

对所以有活动按照开始时间先后来排序。在一个会场内，选定一个活动之后，每下一个被选择的活动都是开始时间最早的，即保证了活动安排的紧凑性。

int count=n,roomavail=0;
//count是仍未被安排的活动数量(初值为活动总数n)，roomavail是当前会场的剩余可分配时间的开始时间点。
	while(count>0)
	{
		//每一个循环都是分配一次新的会场
                for(int i=0;i<n;i++){
			if((meet[i].begin>=roomavail)&&(meet[i].done==0))
                        //meet[].done记录会场是否被安排过
                        //在没被安排过的活动中选择大于等于roomavail的最早的开始时间的活动
			{
				roomavail=meet[i].end;//更新roomavail
				meet[i].done=1;//标记为安排过
				count--;
			}
		}
		roomavail=0;//这个会场已经分配结束。开始新的会场前要将roomavail置为0
		ans++;//会场数++
	}

这个算法与第一题的算法类似，只不过是排序按照开始时间进行的。

第二种

这一种算法写起来看上去很简单，所以比前一种抽象。

#include<bits/stdc++.h>
using namespace std;
int main(){
	int k;         //k:待安排的活动个数
	cin>>k;
	int beg[1001]; //beg[i]:开始时间
	int end[1001]; //end[i]:结束时间 
	for(int i=1;i<=k;i++){
		cin>>beg[i];
		cin>>end[i];
	}
	sort(beg+1,beg+1+k);
	sort(end+1,end+1+k);
	int sum=0;
	int j=1;
	for(int i=1;i<=k;i++){
		if(beg[i]<end[j]){
			sum++;
		}
		else j++;
	}
	cout<<sum;
	return 0; 
}

整个算法乍看上去很叫人迷惑：为什么要对开始时间和结束时间分别排序？这不是割裂了一个活动的开始与结束时间，破坏了整体性？这就是这个算法抽象的地方，接下来我将给出这个算法的解读。

该算法的核心思想是，对于任意一个第i小的开始时间和第j小的结束时间，如果beg[i]>=end[j]，那么以beg[i]为开始时间的活动就可以安排在以end[j]为结束的活动后面；反之则不能，需要开辟新的会场。

结合代码来看

for(int i=1;i<=k;i++){
		if(beg[i]<end[j]){
			sum++;
		}
		else j++;
	}

对于所有的活动(已经按照开始时间排序)，根据其开始时间，该活动可以被安排在

1.某个现有的会场里

2.新开辟的一个会场的开始

这里end[j]记录的是所有已经开辟的会场中剩余可用时间最早的可开始时间。如果当前的beg[i]比end[j]小，这意味着以beg[i]开始的活动不可能安排在任何现存的会场中，即需要开辟一个新会场；反之则可以将该活动安排在以end[j]为结束的活动之后，并且由于这个会场加入了新的活动，结束时间就不再是end[j]，而是以beg[i]开始的活动的结束时间，那么此时所有会场的剩余可用时间最早的可开始时间就从end[j]变为end[j+1]。

举一个简单的例子来反映上述过程

有三个活动：

活动名称 开始时间 结束时间

S1 25 35

S2 27 80

S3 36 50

排序后(不妨设下标从1开始)

beg[]数组：25 27 36

end[]数组：35 50 80

第一步：beg[1]<end[1]。i++，需要开辟新会场1

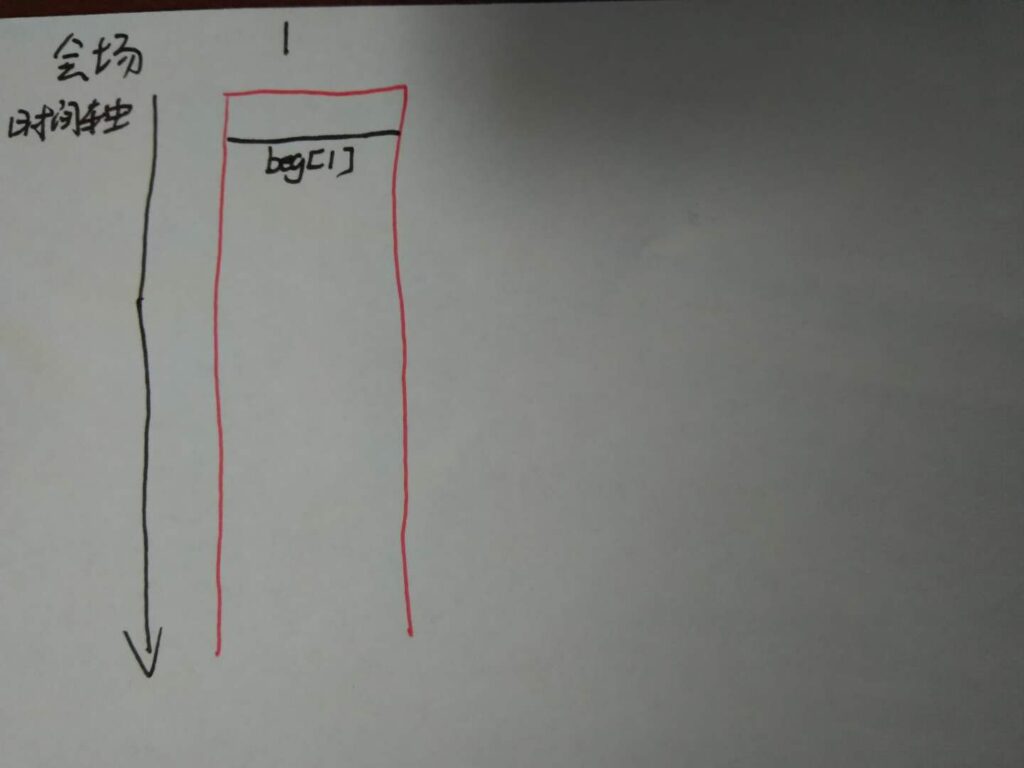
第二步：beg[2]<end[1]。i++，需要开辟新会场2

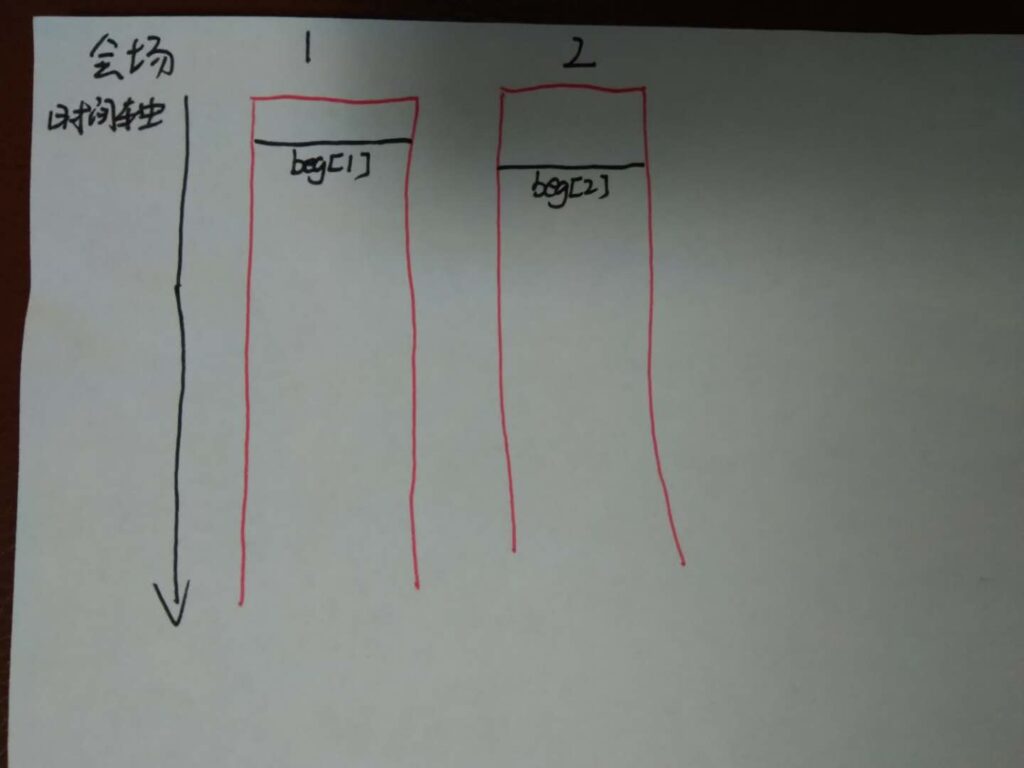
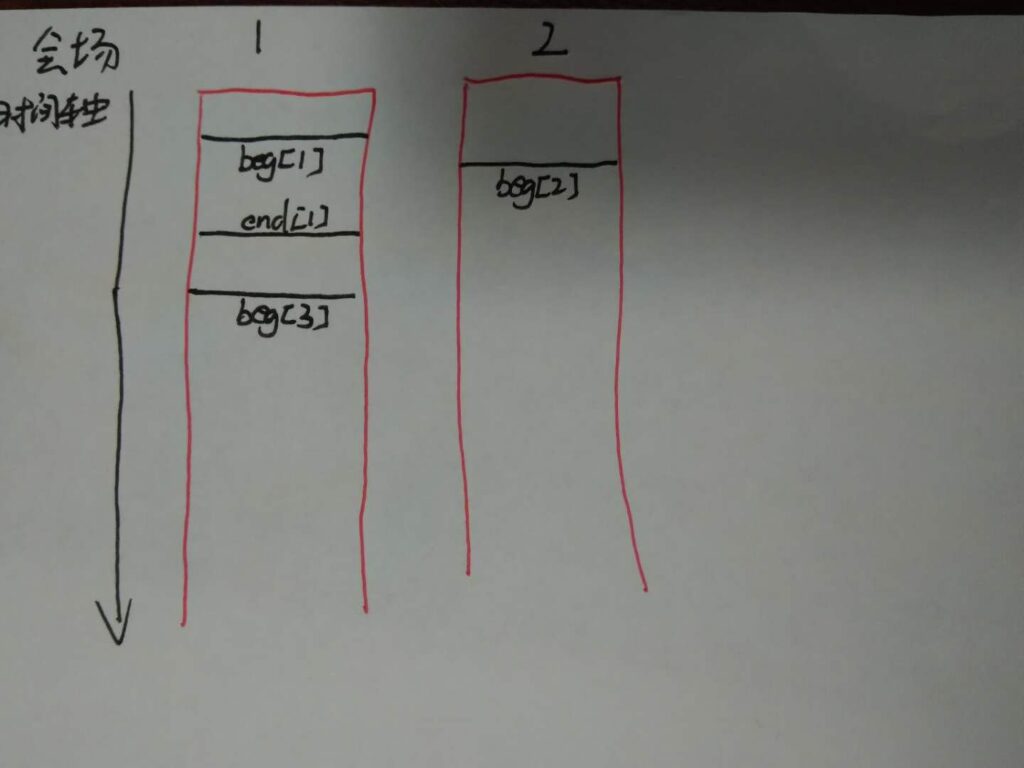
第三步：beg[3]>end[1]。j++，可以将以beg[3]为开始时间的活动安排在会场1或2中。(会场1和会场2中必有一个以end[1]为结束时间的活动，这题中为会场1)

总结

贪心法的证明过程是真的难。