零钱兑换-DP

问题描述

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:

输入: coins = [2], amount = 3
输出: -1
 

说明:
你可以认为每种硬币的数量是无限的。

题解

寻找最优解的问题，很可能和动态规划有关。尤其是这种当前问题的最优解可能分解为子问题，比如求11可分解的零钱的最小个数相当于求（11-任意面值）+1的最小个数。以此类推。

算法：

我们采用自下而上的方式进行思考。仍定义 F(i)F(i) 为组成金额 ii 所需最少的硬币数量，假设在计算 F(i)F(i) 之前，我们已经计算出 F(0)-F(i-1)F(0)−F(i−1) 的答案。 则 F(i)F(i) 对应的转移方程应为

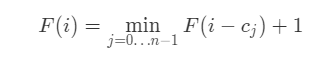
例子1：假设

coins = [1, 2, 5], amount = 11
则，当 i==0时无法用硬币组成，为 0 。当 i<0 时，忽略 F(i)

F(i) 最小硬币数量
F(0) 0 //金额为0不能由硬币组成
F(1)=min(F(1-1),F(1-2),F(1-5))+1=1
F(2)=min(F(2-1),F(2-2),F(2-5))+1=1
F(3)=min(F(3-1),F(3-2),F(3-5))+1=2
F(4)=min(F(4-1),F(4-2),F(4-5))+1=2
… …
F(11)=min(F(11-1),F(11-2),F(11-5))+1=3

代码

/*
    1.动态规划,当前问题的最优解可由子问题得到,
    2.dp[i]=min(dp[i-s1]......dp[i-sn])+1
*/
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
       vector<int> dp(amount+1,amount+1);
        dp[0]=0;
        for(int i=1;i<=amount;i++){
            for(int j=0;j<coins.size();j++){
                if(coins[j]<=i){
                    dp[i]=min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        return dp[amount]>amount?-1:dp[amount];
    }
};

时间复杂度：O(Sn)，其中 S 是金额，n 是面额数。我们一共需要计算 O(S) 个状态，S 为题目所给的总金额。对于每个状态，每次需要枚举 n 个面额来转移状态，所以一共需要 O(Sn) 的时间复杂度。