这篇文章将多项朴素贝叶斯,伯努利朴素贝叶斯,补充朴素贝叶斯,逻辑回归,支持向量机,KNN,决策树,随机森林,梯度提升,神经网络(多层感知机)算法用于垃圾邮件分类,测试比较不同算法的性能,选出适合作为垃圾邮件分类的算法。
测试数据
使用了两个数据集分开测试的,UCI数据集有5574条数据,TREC有37822条数据。
UCI数据集的数据是垃圾短信,TREC是垃圾邮件
UCI相关数据集
https://archive.ics.uci.edu/ml/datasets/sms+spam+collection
邮件数目: 5572 垃圾邮件数目: 747 正常邮件数目: 4825 训练集大小: 4179 测试集大小: 1393
2006 TREC Public Spam Corpora (trec06p)
https://plg.uwaterloo.ca/~gvcormac/treccorpus06/
邮件数目: 37822 垃圾邮件数目: 24912 正常邮件数目: 12910 训练集大小: 28366 测试集大小: 9456
数据集处理
2006 TREC Public Spam Corpora 数据集需要经过处理转化后再进入下面的读入数据,过程看我的另一篇博客:
https://www.cztcode.com/2022/trec-trec06p-dataset-processing/
读入数据
将垃圾邮件spam和正常邮件ham用1,0 标记。
# 读取垃圾邮件数据
data_init = pd.read_table('SMSSpamCollection', sep='\t', names=['label', 'mem'])
# 数据预处理
data_init['label'] = data_init.label.map({'ham': 0, 'spam': 1}) # 0代表正常邮件,1代表垃圾邮件
total_count = data_init.shape[0]
spam_count = np.count_nonzero(data_init['label'].values) # 垃圾邮件数目
print("邮件数目:", total_count)
print("垃圾邮件数目:", spam_count)
print("正常邮件数目:", total_count - spam_count)
划分训练集和测试集
sklearn提供的train_test_split()函数可以将数据拆分为训练集和测试集
random_state=1 表示每次运行得到相同结果(固定划分)
stratify=data_init[‘label’] 表示启用分层拆分,测试集里spam和ham的比例和训练集保持相同
x_train, x_test, y_train, y_test = train_test_split(data_init['mem'], data_init['label'], random_state=1,
stratify=data_init['label'])
print('训练集大小: {}'.format(x_train.shape[0]))
print('测试集大小: {}'.format(x_test.shape[0]))
转化为稀疏矩阵
词袋模型
词袋模型能够把一个句子转化为向量表示,是比较简单直白的一种方法,它不考虑句子中单词的顺序,只考虑词表(vocabulary)中单词在这个句子中的出现次数。
stop_words=’english’ 表示使用内置英语停用词,比如a,the 这种冠词很高频但是对分析无效,所以就直接去掉。
count_vector = CountVectorizer(stop_words='english')
# 学习词汇词典并返回术语 - 文档矩阵(稀疏矩阵)。
train_data = count_vector.fit_transform(x_train)
# 使用符合fit的词汇表或提供给构造函数的词汇表,从原始文本文档中提取词频,转换成词频矩阵
test_data = count_vector.transform(x_test)
先使用fit_transform(x_train)根据停用词表构造出词频矩阵,再使用transform(x_test)把测试集按照已经构造出的词频矩阵的词顺序计算出测试集的词频矩阵。
评估标准
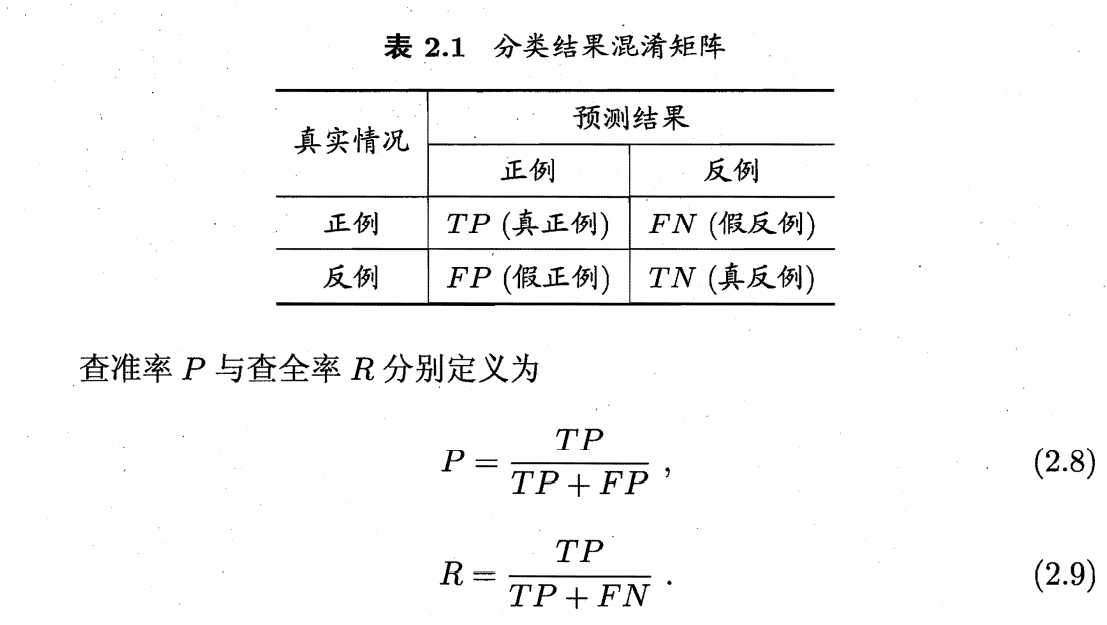
查准率P(正确率(Precision)):垃圾邮件检对率。查准率越高“漏网”的垃圾邮件就越少。
查全率R(召回率(Recall)):垃圾邮件检出率。这个指标反映了过滤系统发现垃圾邮件的能力,查全率反应了过滤系统“找对”垃圾邮件的能力,查全率越大将合法邮件误判为垃圾邮件的可能性越小。
直观地说,精度P是分类器不将负样本标记为正样本的能力,而 召回R是分类器找到所有正样本的能力。
精确率(Accuracy):即对所有邮件(包括垃圾邮件和合法邮件)的判对率。Accuracy=(TP+TN)/N
F1度量:F1实际上是召回率和正确率的调和平均它将召回率和正确率综合成一个指标。F1越大说明模型的效果越好。
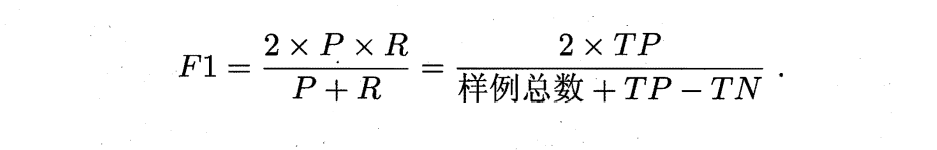
TCR: 人们往往不希望将合法邮件误判成垃圾邮件。为了表示不同情况下垃圾邮件系统的代价Androutsopoulos 等人提出了代价因子的概念。假设将合法邮件误判为垃圾邮件的损失为是垃圾邮件判为合法邮件的 λ倍。比如λ= 9表示一封合法邮件误判的损失是一封垃圾邮件误判的9倍。

这个公式是化简得来的(MarkDown打个公式费多大劲QAQ),TCR 越高表明当前垃圾邮件过滤系统的损失越低。
在测试中测试 λ取2。
在sklearn中输出分类混淆矩阵并计算TCR
sklearn的分类混淆矩阵定义和上面图示的不一样,所以需要加一个label标签转化一下。
https://blog.csdn.net/weixin_34809240/article/details/114439832
y_true = [0, 1, 0, 1, 0, 1, 0];
y_pred = [1, 1, 1, 0, 1, 0, 1];
cm = confusion_matrix(y_true, y_pred, labels=[1, 0]);
TP = cm[0][0]
FP = cm[1][0]
TN = cm[1][1]
FN = cm[0][1]
print("TP:", FP)
print("FP:", FP)
print("TN:", TN)
print("FN:", FN)
输出结果:
TP: 4
FP: 4
TN: 0
FN: 2这里我写了一个计算TCR的函数,k取2
def tcr_score(y_true, y_pred):
cm = confusion_matrix(y_true, y_pred, labels=[1, 0]);
tp = cm[0][0]
fp = cm[1][0]
fn = cm[0][1]
tcr = (tp + fp) / (K * fn + fp)
return tcr比较标准
根据TCR越高的算法分类效果越好,最后按照TCR分值排名。
朴素贝叶斯
关于朴素贝叶斯原理我写过另一篇博客:https://www.cztcode.com/2022/machine-learning-chapter-7/
伯努利、多项式和高斯朴素贝叶斯之间的区别
- MultinomialNB使用出现次数(
频数) - BernoulliNB设计用于
二进制/布尔特征 - GaussianNB用于连续的数据。例如日温度,高度。
高斯分布不适合文本分类,这里就不讨论了。
多项式模型:
设某文档d=(t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则
(1)先验概率P(c)= 类c下样本总数/整个训练样本的样本总数
(2)类条件概率P(tk|c) =(类c下单词tk数目+α)/(指定类下所有特征出现次数之和+类别数*α)
伯努利模型:
(1)先验概率P(c)= 类c下样本总数/整个训练样本的样本总数
(2)类条件概率P(tk|c)=(类c下包含单词tk的文件数+α)/(类c下样本数+类别数*α)
多项式模型和伯努利模型比较
- 贝努利模型不考虑词项出现的次数,而多项式模型考虑
- 贝努利模型适合处理短文档,而多项式模型适合处理长文档
- 贝努利模型在特征数较少时效果更好,而多项式模型在特征较多时效果更好
- 多项式模型:充分考虑了词频的影响,显然的,一篇文章中一个词的词频越高就越有代表性,因此应该考虑词频的影响。 但是,这样的话却避免不了极端数据的影响,比如行中有一行出现100个study,而其他很多行都没有出现study的情况 伯努利模型:实现上比较容易,能降低上述的极端数据的影响
多项式模型朴素贝叶斯分类器
测试结果
参数简介:
alpha*float, default=1.0*
Additive (Laplace/Lidstone) smoothing parameter (0 for no smoothing).
fit_prior*bool, default=True*
Whether to learn class prior probabilities or not. If false, a uniform prior will be used.
class_prior*array-like of shape (n_classes,), default=None*
Prior probabilities of the classes. If specified the priors are not adjusted according to the data.
这里采用了拉普拉斯修正,懒惰学习模式(介绍看上面博客)
# 使用多项朴素贝叶斯模型对数据进行拟合
naive_bayes = MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
naive_bayes.fit(train_data, y_train)
predictions_nb = naive_bayes.predict(test_data)UCI 测试集结果
naive bayes Accuracy score: 0.9870782483847811 naive bayes Precision score: 0.9668508287292817 naive bayes Recall score: 0.9358288770053476 naive bayes F1 score: 0.951086956521739 naive bayes TCR score: 6.033333333333333
TREC测试集结果
naive bayes Accuracy score: 0.9685913705583756 naive bayes Precision score: 0.9920358387257342 naive bayes Recall score: 0.960019267822736 naive bayes F1 score: 0.9757649938800491 naive bayes TCR score: 11.038461538461538
伯努利朴素贝叶斯分类器
测试结果
# 伯努利朴素贝叶斯模型数据拟合
b_naive_bayes = BernoulliNB(alpha=1.0, class_prior=None, fit_prior=True)
b_naive_bayes.fit(train_data, y_train)
b_predictions_nb = b_naive_bayes.predict(test_data)
UCI 测试集结果
Bernoulli bayes Accuracy score: 0.9712849964106246 Bernoulli bayes Precision score: 1.0 Bernoulli bayes Recall score: 0.786096256684492 Bernoulli bayes F1 score: 0.8802395209580839 Bernoulli bayes TCR score: 1.8375
TREC 测试集结果
Bernoulli bayes Accuracy score: 0.9065143824027073 Bernoulli bayes Precision score: 0.881061038220194 Bernoulli bayes Recall score: 0.9919717405266538 Bernoulli bayes F1 score: 0.9332326283987916 Bernoulli bayes TCR score: 7.507494646680942
补充朴素贝叶斯分类器
sklearn还提供优化的朴素贝叶斯分类器,一同测试一下。
CNB是标准多项式朴素贝叶斯(MNB)算法的一种自适应算法,特别适用于不平衡的数据集。具体而言,CNB使用来自每个类的补充的统计数据来计算模型的权重。CNB的发明者经验性地表明,CNB的参数估计比MNB的参数估计更稳定。此外,CNB在文本分类任务方面经常优于MNB(通常以相当大的幅度)。
# 使用补充朴素贝叶斯模型对数据进行拟合
c_naive_bayes = ComplementNB(alpha=1.0, class_prior=None, fit_prior=True)
c_naive_bayes.fit(train_data, y_train)
c_predictions_nb = c_naive_bayes.predict(test_data)
UCI 测试集结果
complement bayes Accuracy score: 0.9712849964106246 complement bayes Precision score: 0.8483412322274881 complement bayes Recall score: 0.9572192513368984 complement bayes F1 score: 0.899497487437186 complement bayes TCR score: 4.395833333333333
TREC 测试集结果
complement bayes Accuracy score: 0.9588620981387479 complement bayes Precision score: 0.9979532662459492 complement bayes Recall score: 0.9394669235709698 complement bayes F1 score: 0.967827309569101 complement bayes TCR score: 7.654046997389034
朴素贝叶斯分类总结
按照TCR排名,最好的是多项式模型朴素贝叶斯分类器,其次是补充朴素贝叶斯分类器,最差的是伯努利朴素贝叶斯分类器。当使用样本数更多的TREC数据集后,伯努利朴素贝叶斯和补充朴素贝叶斯的分类效果接近,数据集的增加对伯努利朴素贝叶斯分类效果提升明显。
补充朴素贝叶斯分类器效果比多项式模型差。
KNN算法
一文搞懂k近邻(k-NN)算法(一) – 忆臻的文章 – 知乎 https://zhuanlan.zhihu.com/p/25994179
KNN算法(k近邻算法):k近邻算法是一种基本分类和回归方法。给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
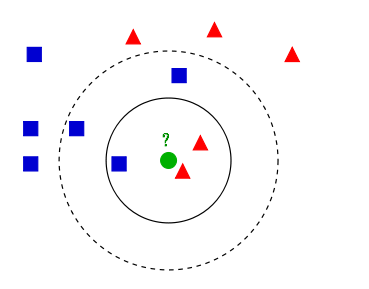
如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的,来了一个新的数据点,我要得到它的类别是什么?好的,下面我们根据k近邻的思想来给绿色圆点进行分类。
- 如果K=3,绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果K=5,绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
K值的选取
选取较小的k值会意味着我们的整体模型会变得复杂,容易发生过拟合
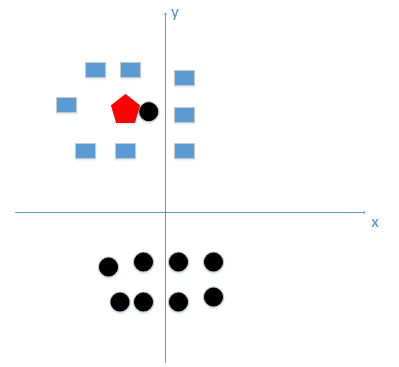
比如这种情况K等于1时会分类到黑色原点,也就是学习到了噪声,过拟合。
所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低,经过上例,我们可以得到k太小会导致过拟合,很容易将一些噪声(如上图离五边形很近的黑色圆点)学习到模型中,而忽略了数据真实的分布!
如果我们选取较大的k值,就相当于用较大邻域中的训练数据进行预测,这时与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误,k值的增大意味着整体模型变得简单。
所以K值在下面红色园边界之内是最好的
距离的度量
k近邻算法是在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,我们就说预测点属于哪个类。
定义中所说的最邻近是如何度量呢?我们怎么知道谁跟测试点最邻近。这里就会引出我们几种度量俩个点之间距离的标准。
我们可以有以下几种度量方式:

其中当p=2的时候,就是我们最常见的欧式距离,我们也一般都用欧式距离来衡量我们高维空间中俩点的距离。在实际应用中,距离函数的选择应该根据数据的特性和分析的需要而定,一般选取p=2欧式距离表示,这不是本文的重点。
恩,距离度量我们也了解了,下面我要说一下各个维度归一化的必要性!
3.特征归一化的必要性
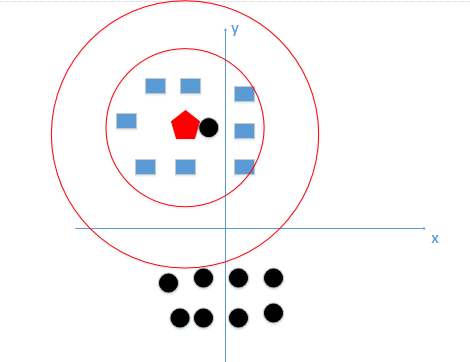
首先举例如下,我用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]
通过上述训练样本,我们看出问题了吗?
很容易看到第一维身高特征是第二维脚码特征的4倍左右,那么在进行距离度量的时候,我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的,最终可能会导致距离计算错误,从而导致预测错误。口说无凭,举例如下:
现在我来了一个测试样本 F(167,43),让我们来预测他是男性还是女性,我们采取k=3来预测。
下面我们用欧式距离分别算出F离训练样本的欧式距离,然后选取最近的3个,多数类别就是我们最终的结果,计算如下:
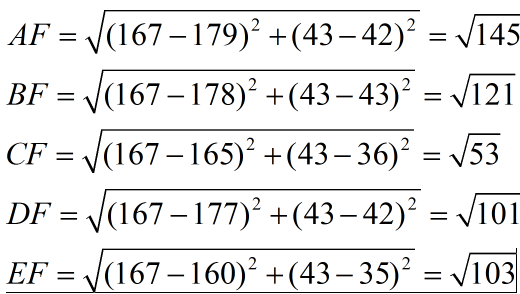
由计算可以得到,最近的前三个分别是C,D,E三个样本,那么由C,E为女性,D为男性,女性多于男性得到我们要预测的结果为女性。
这样问题就来了,一个女性的脚43码的可能性,远远小于男性脚43码的可能性,那么为什么算法还是会预测F为女性呢?那是因为由于各个特征量纲的不同,在这里导致了身高的重要性已经远远大于脚码了,这是不客观的。所以我们应该让每个特征都是同等重要的!这也是我们要归一化的原因!归一化公式如下:

测试结果
用sklearn提供的knn分类器进行分类。这里的k取1,我试过了k取的越大,F1的值越低,所以最好的结果就是n_neighbors取1。
# KNN算法
k_neighbor = KNeighborsClassifier(n_neighbors=1, weights='uniform')
k_neighbor.fit(train_data, y_train)
predictions_knn = k_neighbor.predict(test_data)
UCI 测试集结果
knn Accuracy score: 0.9533381191672649 knn Precision score: 1.0 knn Recall score: 0.6524064171122995 knn F1 score: 0.7896440129449839 knn TCR score: 0.9384615384615385

我没看出来KNN和朴素贝叶斯比性能可以相当。。。 k取较小值性能较好是真的。
结论: KNN不太适合用于垃圾邮件分类,召回率太低会导致垃圾邮件检出率低,F1得分和TCR得分都很低。
TREC 测试集结果
使用trec06p更大的数据集后,knn的效果果然和朴素贝叶斯相当了
邮件数目: 37822 垃圾邮件数目: 24912 正常邮件数目: 12910 邮件正文缺失数目: 0 训练集大小: 28366 测试集大小: 9456 knn Accuracy score: 0.9588620981387479 knn Precision score: 0.9712671509281678 knn Recall score: 0.9661207450224791 knn F1 score: 0.9686871126137003 knn TCR score: 10.325
多项朴素贝叶斯的成绩
naive bayes Accuracy score: 0.9685913705583756 naive bayes Precision score: 0.9920358387257342 naive bayes Recall score: 0.960019267822736 naive bayes F1 score: 0.9757649938800491 naive bayes TCR score: 11.038461538461538
真的相差无几
结论::knn在样本集更大时和朴素贝叶斯有相近的性能,但是knn分类的速度要慢于朴素贝叶斯。
SVM
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
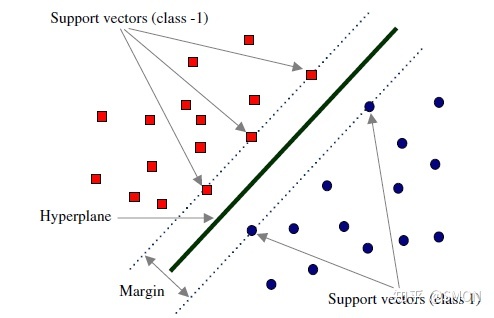
在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用。如果移动非支持向量,甚至删除非支持向量都不会对最优超平面产生任何影响。也即支持向量对模型起着决定性的作用,这也是“支持向量机”名称的由来。
SVM算法的主要优点有:
- 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。
- 仅仅使用一部分支持向量来做超平面的决策,无需依赖全部数据。
- 有大量的核函数可以使用,从而可以很灵活的来解决各种非线性的分类回归问题。
- 样本量不是海量数据的时候,分类准确率高,泛化能力强。
SVM算法的主要缺点有:
- 如果特征维度远远大于样本数,则SVM表现一般。
- SVM在样本量非常大,核函数映射维度非常高时,计算量过大,不太适合使用。
- 非线性问题的核函数的选择没有通用标准,难以选择一个合适的核函数。
- SVM对缺失数据敏感。
测试结果
UCI 测试集结果
support vector machine Accuracy score: 0.9806173725771715 support vector machine Precision score: 1.0 support vector machine Recall score: 0.8556149732620321 support vector machine F1 score: 0.9221902017291067 support vector machine TCR score: 2.962962962962963
TREC 测试集结果
support vector machine Accuracy score: 0.8212774957698815 support vector machine Precision score: 0.7880904012188928 support vector machine Recall score: 0.9966281310211946 support vector machine F1 score: 0.8801758366420874 support vector machine TCR score: 4.603156049094097
LinearSVC
svm_clf = svm.LinearSVC()
svm_clf.fit(train_data, y_train)
predictions_svm = svm_clf.predict(test_data)
测试结果
UCI 测试集结果
support vector machine Accuracy score: 0.9820531227566404 support vector machine Precision score: 0.9939024390243902 support vector machine Recall score: 0.8716577540106952 support vector machine F1 score: 0.9287749287749287 support vector machine TCR score: 3.3469387755102042
TREC 测试集结果
support vector machine Accuracy score: 0.9845600676818951 support vector machine Precision score: 0.9814756174794174 support vector machine Recall score: 0.9953436095054592 support vector machine F1 score: 0.9883609693877551 support vector machine TCR score: 36.09142857142857
结论:在垃圾邮件过滤任务中,大量实验表明线性核表现出很高的性能,与其他核函数的性能相近。而对线性核进行合适的特征表示可获取较佳的分类性能和较低的计算复杂度。
逻辑回归
逻辑回归介绍:https://zhuanlan.zhihu.com/p/74874291
测试结果
UCI 测试集结果
logistic regression Accuracy score: 0.9791816223977028 logistic regression Precision score: 1.0 logistic regression Recall score: 0.8449197860962567 logistic regression F1 score: 0.9159420289855073 logistic regression TCR score: 2.7241379310344827
TREC 测试集结果
logistic regression Accuracy score: 0.9849830795262268 logistic regression Precision score: 0.9811827956989247 logistic regression Recall score: 0.9963070006422607 logistic regression F1 score: 0.9886870618228171 logistic regression TCR score: 38.32727272727273
决策树
决策树是一种逻辑简单的机器学习算法,它是一种树形结构,所以叫决策树。
决策树简介:https://easyai.tech/ai-definition/decision-tree/
decision_tree = DecisionTreeClassifier()
decision_tree.fit(train_data, y_train)
predictions_dt = decision_tree.predict(test_data)
测试结果
UCI 测试集结果
decision tree Accuracy score: 0.9698492462311558 decision tree Precision score: 0.9190751445086706 decision tree Recall score: 0.8502673796791443 decision tree F1 score: 0.8833333333333333 decision tree TCR score: 2.4714285714285715
TREC 测试集结果
decision tree Accuracy score: 0.9755710659898477 decision tree Precision score: 0.9731734259113145 decision tree Recall score: 0.9902055234425177 decision tree F1 score: 0.981615598885794 decision tree TCR score: 21.70205479452055
随机森林
随机森林是由很多决策树构成的,不同决策树之间没有关联。当我们进行分类任务时,新的输入样本进入,就让森林中的每一棵决策树分别进行判断和分类,每个决策树会得到一个自己的分类结果,决策树的分类结果中哪一个分类最多,那么随机森林就会把这个结果当做最终的结果。
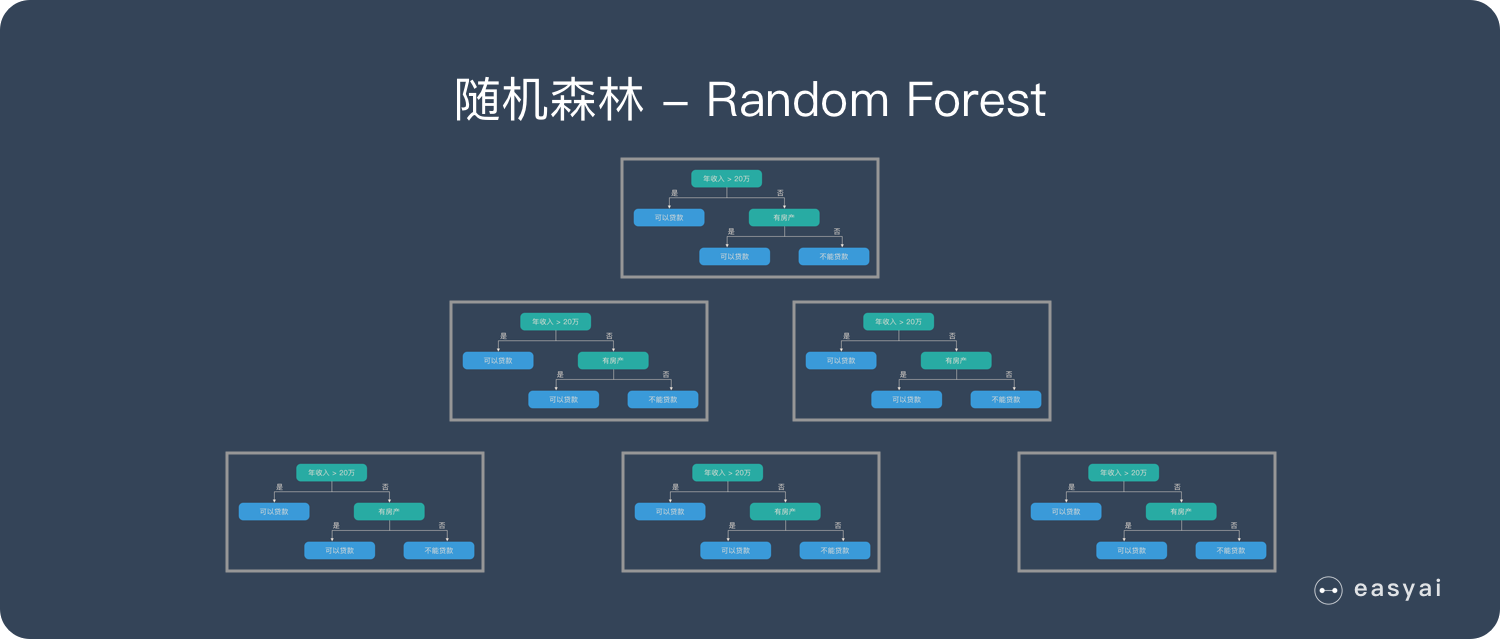
随机森林介绍:https://easyai.tech/ai-definition/random-forest/
测试结果
random_forest = RandomForestClassifier()
random_forest.fit(train_data, y_train)
predictions_rf = random_forest.predict(test_data)
UCI 测试集结果
random forest Accuracy score: 0.9755922469490309 random forest Precision score: 1.0 random forest Recall score: 0.8181818181818182 random forest F1 score: 0.9 random forest TCR score: 2.25
TREC 测试集结果
random forest Accuracy score: 0.9865693739424704 random forest Precision score: 0.9895682875942866 random forest Recall score: 0.9900449582530507 random forest F1 score: 0.9898065655349547 random forest TCR score: 32.96825396825397
Gradient Boosting
gdbt = GradientBoostingClassifier()
gdbt.fit(train_data, y_train)
predictions_gdbt = gdbt.predict(test_data)
测试结果
Gradient Boosting:https://zhuanlan.zhihu.com/p/26327929
UCI 测试集结果
gradient boosting Accuracy score: 0.9619526202440776 gradient boosting Precision score: 0.9926470588235294 gradient boosting Recall score: 0.7219251336898396 gradient boosting F1 score: 0.8359133126934984 gradient boosting TCR score: 1.2952380952380953
TREC 测试集结果
gradient boosting Accuracy score: 0.9526226734348562 gradient boosting Precision score: 0.9376135675348274 gradient boosting Recall score: 0.9942196531791907 gradient boosting F1 score: 0.9650872817955112 gradient boosting TCR score: 13.644628099173554
神经网络
多层感知器的优点包括:
- 学习非线性模型的能力。
- 实时学习模型的能力(在线学习)
partial_fit。
多层感知器的缺点包括:
- 具有隐藏层的MLP非凸性损失函数,其中存在多个局部最小值。因此,不同的随机权重初始化可能导致不同的精度。
- MLP需要调整许多超参数,例如隐藏神经元的数量,层数和迭代次数。
- MLP对特征缩放很敏感。
[ 分享 ] Sklearn 中的神经网络 Neural network models – napher的文章 – 知乎 https://zhuanlan.zhihu.com/p/352330001
从线性回归到逻辑回归再到人工神经网络:http://lijinglin.cn/index.php/archives/21.html
求解器*{‘lbfgs’,’sgd’,’adam’},默认 =’adam’*
权重优化的求解器。
- ‘lbfgs’ 是准牛顿方法家族中的优化器。
- ‘sgd’ 指的是随机梯度下降。
- “adam”指的是由 Kingma、Diederik 和 Jimmy Ba 提出的基于随机梯度的优化器
注意:就训练时间和验证分数而言,默认求解器“adam”在相对较大的数据集(具有数千个训练样本或更多)上运行良好。然而,对于小型数据集,“lbfgs”可以更快地收敛并表现更好。
UCI测试集使用lbfgs,TREC测试集使用adam
mlp = MLPClassifier(solver='lbfgs', activation='logistic')
mlp.fit(train_data, y_train)
predictions_nn = mlp.predict(test_data)
测试结果
UCI 测试集结果
neural network Accuracy score: 0.9863603732950467 neural network Precision score: 0.9772727272727273 neural network Recall score: 0.9197860962566845 neural network F1 score: 0.9476584022038568 neural network TCR score: 5.176470588235294
TREC 测试集结果
neural network Accuracy score: 0.9884729272419628 neural network Precision score: 0.9869489097564857 neural network Recall score: 0.9956647398843931 neural network F1 score: 0.9912876668531693 neural network TCR score: 46.1985294117647
总结
TCR分数
| 算法 | naive bayes | complement bayes | Bernoulli bayes | logistic regression | support vector machine | knn | decision tree | random forest | gradient boosting TCR score | neural network TCR score |
|---|---|---|---|---|---|---|---|---|---|---|
| SPEC TCR 得分 | 11.03 | 7.65 | 7.5 | 38.32 | 36.09 | 10 | 21.91 | 33.17 | 13.64 | 46.19 |
| UCI TCR得分 | 6.03 | 4.39 | 1.83 | 2.72 | 3.34 | 0.9 | 2.47 | 2.42 | 1.25 | 4.09 |
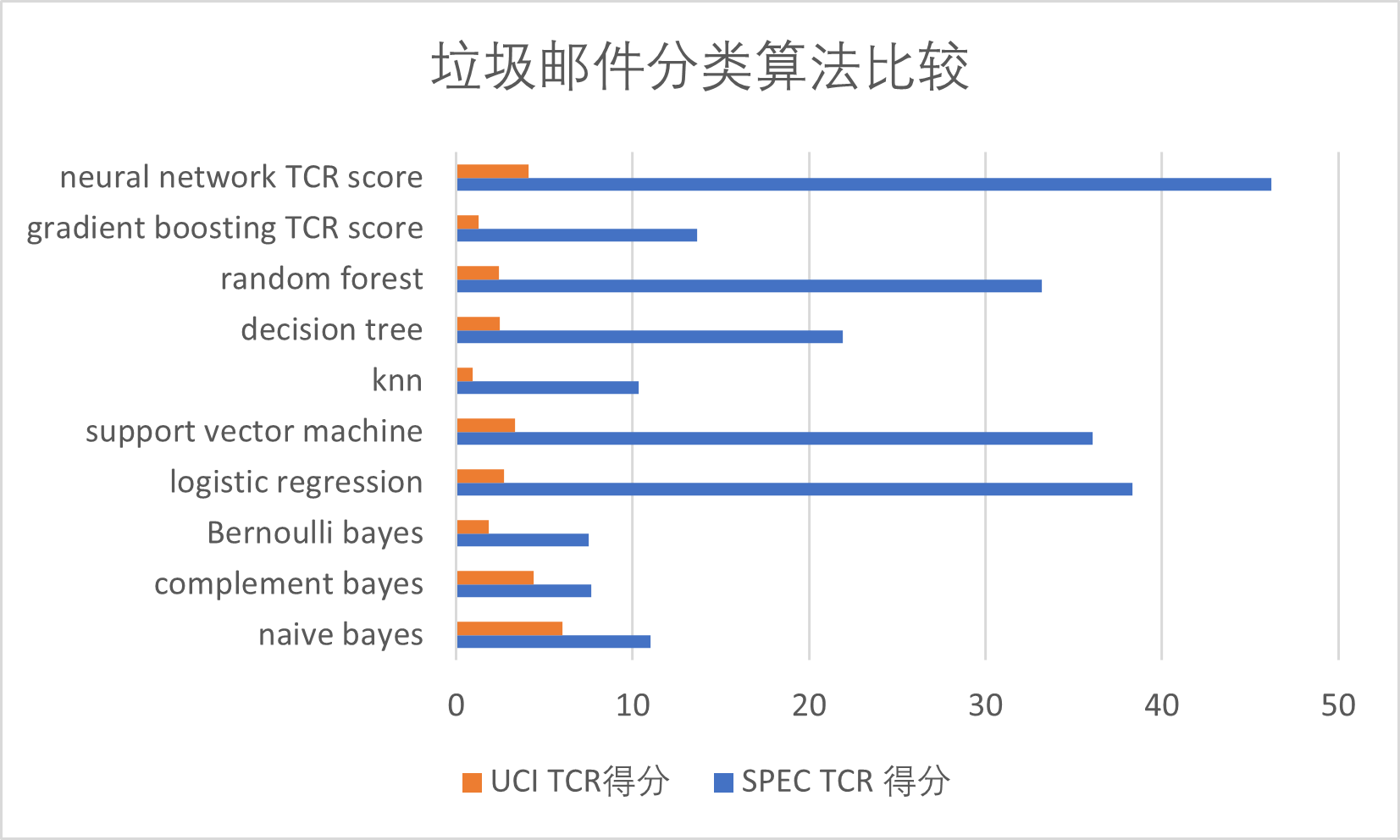
可以看出神经网络在数据集更大时有更好的分类效果,当数据集较小时,多项朴素贝叶斯有着更快的分类速度和更好的分类结果。
使用神经网络进行分类还可以对模型进行增量更新,适合对一定样本进行训练后再通过用户手动标记垃圾邮件获取更精确的分类结果。