“科大讯飞杯”C题总结

张老师的旅行

链接：https://ac.nowcoder.com/acm/contest/5477/C
来源：牛客网

题目描述

张老师到了一个王国去旅游，王国有n个景点，张老师到达这个城市所在的车站恰好位于第x个景点，这个王国非常特别，恰好所有著名的景点都在分布在直线上，每个景点在坐标p_i上(单位：公里)，张老师身体非常好，每走一公里花费一分钟。每个景点都有一个打卡点，并且必须在不迟于相应的时间（时间从张老师到达王国开始计算）前到达才能打卡成功并且给以一个打卡标记，集齐所这些标记就能获得一个大礼包。由于张老师非常想要大礼包，并且因为张老师还着急去下一个王国旅游，所以张老师希望用的时间尽量少，你能帮帮张老师吗？

输入描述:

输入的第一行，包含一个整数n（1≤n≤1000）。
第二行包含n个整数pi(1≤pi≤100000)，第i个整数pi为第i个景点的坐标（坐标从小到大排列）。
最后一行包含n个整数ti(0≤ti≤10,000,000)，ti表示第i个景点最迟到达的时间，时间为0则表示张老师所在车站的位置且只有一个为0。

输出描述:

输出所需的最少时间，若无解输出-1。

输入

4
1 2 3 4
0 1 2 3

输出

3

AC代码

用动态规划，dp[i][j][0/1]，其中i为起点左边第i个的景点，j为起点右边第j个的景点，dp[i][j]是张老师走完左边i个和右边j个所花费的时间。所以要对所有景点分为左右两组，并且由于所有景点在一条直线上，访问远处的景点必会经过近处的景点，所以要按照距离起点的距离排序。本题输入已经按照绝对距离大小给出了，所以对输入稍微处理一下就行。

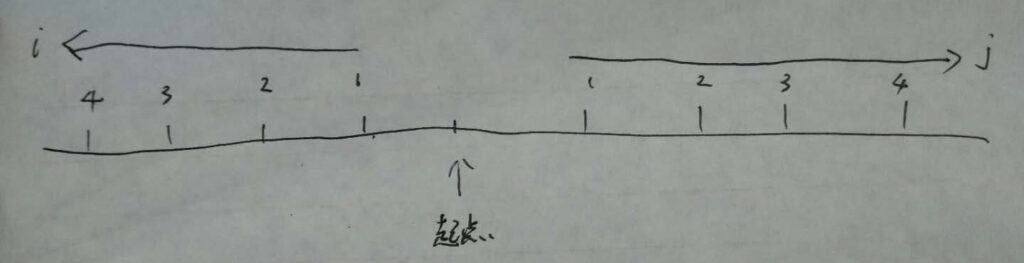
dp数组的第三个维度表示落脚点，取值为0或1，0表示落脚点在起点第i个景点，1表示落脚点在起点右边第j个景点。例如dp[i][j][0]指这一步是走到左边第i个景点，dp[i][j][1]指这一步走到右边第j个景点。那么对于dp[i][j][0]来说，上一步张老师必然在左边第i-1个景点，或者右边第j个景点。dp[i][j][0]表达式(dp[i][j][1]同理)为

dp[i][j][0]=min(dp[i-1][j][0]+left[i].pos-left[i-1].pos,dp[i-1][j][1]+right[j].pos+left[i].pos);
dp[i][j][1]=min(dp[i][j-1][0]+left[i].pos+right[j].pos,dp[i][j-1][1]+right[j].pos-right[j-1].pos);

之后就是限定条件：到达每个经典不得超过最迟时间。那就是第三维下标为0的，必须小于i的时间，下标为1的必须小于j的时间。如果对于任意一个dp[i][j]，无论落脚点在左边还是右边，都不符合时间限制，那么说明张老师不可能在规定时间内访问到从左边第i个到右边第j个，此时输出无解。如果只有一个情况不可能，就将其设置为无限大，以限定以后的情况。

#include<stdio.h>
#include<string.h>
using namespace std;
struct place
{
	int time;//时间 
	int pos;//位置 
}scene[1001],left[1001],right[1001];
const int inf = 0x3f3f3f3f;
int begin,leftn=0,rightn=0,n;
int dp[1001][1001][2];
int min(int x,int y)
{
	return (x>y?y:x);
}
int main()
{
	memset(dp,inf,sizeof(dp));
	scanf("%d",&n);
	for (int i=0;i<n;i++)
	{
		scanf("%d",&scene[i].pos);	
	}
	for (int i=0;i<n;i++)
	{
		scanf("%d",&scene[i].time);
		if (scene[i].time==0)
		{
			begin=i;//记录起点 
		}
	}
	//生成位于起点左边和右边的景点距离和时间 
	for (int i=begin-1;i>=0;i--)
	{
		leftn++;
		left[leftn].time=scene[i].time;
		left[leftn].pos=scene[begin].pos-scene[i].pos;
	}
	
	for (int i=begin+1;i<n;i++)
	{
		rightn++;
		right[rightn].time=scene[i].time;
		right[rightn].pos=scene[i].pos-scene[begin].pos;
	}
	dp[0][0][0]=0;dp[0][0][1]=0;
	for (int i=0;i<=leftn;i++)
	{
		for (int j=0;j<=rightn;j++)
		{
			if (i)	dp[i][j][0]=min(dp[i-1][j][0]+left[i].pos-left[i-1].pos,dp[i-1][j][1]+right[j].pos+left[i].pos);
			if (j)	dp[i][j][1]=min(dp[i][j-1][0]+left[i].pos+right[j].pos,dp[i][j-1][1]+right[j].pos-right[j-1].pos);
			if (dp[i][j][0]>left[i].time&&dp[i][j][1]>right[j].time)
			{
				printf("-1\n");
				return 0;
			}
			if (dp[i][j][0]>left[i].time)	dp[i][j][0]=inf;
			if (dp[i][j][1]>right[j].time)	dp[i][j][1]=inf;
		}
	}
	printf("%d\n",min(dp[leftn][rightn][0],dp[leftn][rightn][1]));
	return 0;
 } 

反思

这一题我看到数据范围就知道不能暴力搜了，但是又苦于想不出动规的解法，于是索性就先暴力搜看看，找找思路。显然是过不掉的，但是剪完枝之后的通过率（33.3%）比剪枝前（50%）还低是我没想到的。

对于这个题目，数据范围已经决定了暴力搜是做不了的。而我因为掌握的动规模型少之又少，并且这一题的限界条件在我看来不是很好处理，于是很尴尬地僵住了。

动态规划这种东西，就是你想到了就简单，想不到就完了。我决定以这道题为起点，开始去多接触些动态规划的题目。