n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
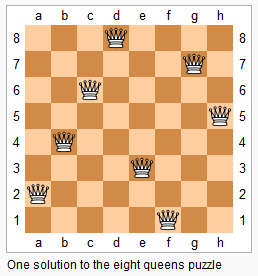
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。提示:
题解
n皇后是典型的回溯法问题。通过回溯法找到求解问题的所有子节点(解空间),若当前节点不符合条件,则回退到上一个节点。
/*
* @lc app=leetcode.cn id=51 lang=cpp
*
* [51] N皇后
*/
// @lc code=start
class Solution {
public:
vector<vector<string>> ans;
vector<vector<string>> solveNQueens(int n) {
vector<string> ans_one(n, string(n, '.')); //以.开始初始化
dfs(ans_one, 0);
return ans;
}
void dfs(vector<string> &ans_one, int row) {
int n = ans_one.size();
if (row == n) { //回溯出口
ans.push_back(ans_one);
return;
}
for (int col = 0; col < n; col++) {
if (!valid(ans_one, row, col)) continue;
ans_one[row][col] = 'Q';
dfs(ans_one, row + 1); //送入下层循环
ans_one[row][col] = '.'; //回退到上个节点
}
}
bool valid(vector<string> &ans_one, int row, int col) {
int n = ans_one.size();
//看当前列是否有皇后
for (int i = 0; i < row; i++) {
if (ans_one[i][col] == 'Q') return false;
}
//寻找右上部分的皇后,看是否重复
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (ans_one[i][j] == 'Q') return false;
}
//寻找左上部分的皇后,看是否重复
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (ans_one[i][j] == 'Q') return false;
}
return true;
}
};
// @lc code=end
注意这里ans_one使用的必须为引用类型,因为是对同一个地址操作,不需要复制值再去操作,后者会很浪费时间。
若ans_one不为引用类型,执行时间为:
Accepted
- 9/9 cases passed (180 ms)
- Your runtime beats 5.44 % of cpp submissions
- Your memory usage beats 5.55 % of cpp submissions (50.6 MB)
引用类型则为:
Accepted
- 9/9 cases passed (8 ms)
- Your runtime beats 88.1 % of cpp submissions
- Your memory usage beats 100 % of cpp submissions (7.7 MB)