给定一个正整数和负整数组成的 N × M 矩阵,编写代码找出元素总和最大的子矩阵。
返回一个数组 [r1, c1, r2, c2],其中 r1, c1 分别代表子矩阵左上角的行号和列号,r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵,返回任意一个均可。
注意:本题相对书上原题稍作改动
输入:
[
[-1,0],
[0,-1]
]
输出: [0,1,0,1]
解释: 输入中标粗的元素即为输出所表示的矩阵
说明:
1 <= matrix.length, matrix[0].length <= 200
来源:力扣(LeetCode)
题解
最大子矩阵,可以先转化为求一行的最大字序列和,通过把这个问题升到二维解决。本题是一个DP问题。
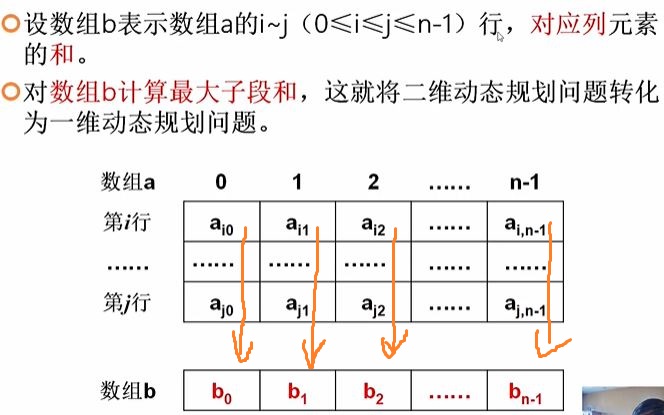
其实具体算法在算法书上已经有了,只不过书上的例题在均为负数时,最大值为0。而这道题如果均为负数,还要输出最大的负数,所以只要做一个小改动就好了,我写了一个算法,同时LeetCode上面还有一个更好的算法,在这里简单讲解一下。
先看我写的(嘿嘿)
#include <iostream>
#include <vector>
using namespace std;
#define r 2
#define l 2
class Solution {
public:
int maxSubArray(vector<int>& nums, int& c1, int& c2) {
int b = 0, sum = INT_MIN,c1_temp;
for (int i = 0; i < nums.size(); i++) {
if (b > 0) {
b += nums[i];
} else {
b = nums[i];
c1_temp = i;
}
if (b > sum ) {
sum = b;
c2 = i;
c1=c1_temp;
}
}
return sum;
}
vector<int> getMaxMatrix(vector<vector<int>>& matrix) {
int max, c1, c2, r1, r2, Max_final = INT_MIN, c1_final, c2_final;
r1 = r2 = c1_final = c2_final =c1=c2= 0;
vector<int> ans(4);
for (int i = 0; i < matrix.size(); i++) {
vector<int> li(matrix[0].size()); //默认值为0
for (int j = i; j < matrix.size(); j++) {
for (int k = 0; k < matrix[0].size(); k++) {
li[k] += matrix[j][k];
}
max = maxSubArray(li, c1, c2);
if (max > Max_final) {
Max_final = max;
r1 = i, r2 = j;
c1_final = c1, c2_final = c2;
}
}
}
ans[0] = r1;
ans[1] = c1_final;
ans[2] = r2;
ans[3] = c2_final;
return ans;
}
};
int main() {
int array[r][l] = {-1, 0,0,-1};
vector<vector<int>> matrix(r, vector<int>(l));
for (int i = 0; i < r; i++) {
for (int j = 0; j < l; j++) {
matrix[i][j] = array[i][j];
}
}
Solution s;
s.getMaxMatrix(matrix);
}因为自己测试了一下,实际上的算法只有class中的内容。
maxSubArray用来计算一行的字序列最大值,输出列的范围
getMaxMatrix通过调用maxSubArray,实现矩阵的计算。
这个方法稍微有点麻烦在于,其实maxSubArray可以写进getMaxMatrix里,就有了下面这个程序,核心思想都是一样的。
更新了算法的格式
这样写比上面的更简洁
/*
1.动态规划,压缩成行矩阵
*/
#include <iostream>
#include <vector>
using namespace std;
int main() {
int m, n, MAX = 0, init_n, end_n;
cin >> m >> n;
vector<vector<int>> vec(m, vector<int>(n));
vector<int> ans(4);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> vec[i][j];
}
}
for (int i = 0; i < m; i++) {
vector<int> dp(n);
for (int j = i; j < m; j++) {
int sum = 0, b = 0;
for (int k = 0; k < n; k++) {
dp[k] += vec[j][k];
if (b > 0) {
b += dp[k];
} else {
b = dp[k];
init_n = k;
}
if (b > sum) {
sum = b;
end_n = k;
}
}
if (sum > MAX) {
MAX = sum;
ans[0] = i;
ans[1] = j;
ans[2] = init_n;
ans[3] = end_n;
}
}
}
cout << MAX<<endl;
cout<<ans[0]+1;
for(int i=1;i<4;i++){
cout<<' '<<ans[i]+1;
}
system("pause");
}每次移动k时计算当前列的最大序列,加完一行直接计算完成,减小了时间复杂度,也增加了程序的可读性。
就到这里,有兴趣的可以再去实现一下。